কালীন সারি (Time Series)

সংজ্ঞা:
কালীন সারি (Time Series) হলো একটি চলকের মান যা সময়ের বিভিন্ন বিন্দুতে সংগ্রহ করা হয়। এটি সময়ের উপর ভিত্তি করে ডেটা বিশ্লেষণের একটি পরিসংখ্যানিক পদ্ধতি, যা ভবিষ্যদ্বাণী এবং প্রবণতা নির্ধারণের জন্য ব্যবহৃত হয়।

কালীন সারির মূল উপাদান

১. প্রবণতা (Trend):
এটি ডেটাসেটের দীর্ঘমেয়াদি সাধারণ গতি বা দিক নির্দেশ করে।
উদাহরণ: জনসংখ্যার ক্রমবর্ধমান হার।

২. ঋতুপ্রভাব (Seasonal Variation):
এটি ডেটার পুনরাবৃত্ত চক্রের মতো আচরণ যা নিয়মিত সময়ের ব্যবধানে ঘটে।
উদাহরণ: গ্রীষ্মকালে এয়ার কন্ডিশনার বিক্রয়ের বৃদ্ধি।

৩. চক্রগত পার্থক্য (Cyclic Variation):
এটি দীর্ঘমেয়াদি অর্থনৈতিক বা অন্য কোনো চক্রগত ওঠানামা নির্দেশ করে।
উদাহরণ: ব্যবসায়িক চক্র।

৪. অস্বাভাবিকতা (Irregular Variation):
এটি ডেটায় আকস্মিক বা অনিয়মিত পরিবর্তন যা কোনো নির্দিষ্ট প্যাটার্ন অনুসরণ করে না।
উদাহরণ: প্রাকৃতিক দুর্যোগের কারণে পণ্যের দামের পরিবর্তন।

কালীন সারি বিশ্লেষণের পদ্ধতি

১. গ্রাফিকাল পদ্ধতি (Graphical Method):
সময়ের বিপরীতে ডেটাকে চিত্রায়িত করে প্রবণতা এবং পরিবর্তন বোঝা।

২. গড় পদ্ধতি (Averaging Method):
ডেটার মসৃণতা বা প্রবণতা নির্ধারণ করতে চলমান গড় (Moving Average) ব্যবহার করা।

3. ম্যাট্রিক্স পদ্ধতি (Decomposition Method):
   কালীন সারিকে এর উপাদানগুলিতে ভাগ করে বিশ্লেষণ করা।
4. পরিসংখ্যানিক মডেল (Statistical Models):
   ভবিষ্যদ্বাণী করার জন্য লিনিয়ার রিগ্রেশন, আরিমা (ARIMA), বা অন্যান্য সময় সিরিজ মডেল ব্যবহার করা।

কালীন সারির ব্যবহার

১. ব্যবসা ও অর্থনীতি:
বিক্রয় প্রবণতা, মুনাফা পূর্বাভাস, এবং বাজার বিশ্লেষণে।

২. পরিবহন:
যাত্রী প্রবাহ বিশ্লেষণ এবং যানজট পূর্বাভাসে।

৩. আবহাওয়া পূর্বাভাস:
তাপমাত্রা, বৃষ্টিপাত, এবং আবহাওয়ার পরিবর্তন বিশ্লেষণে।

৪. স্বাস্থ্য:
রোগের প্রকোপ এবং ঋতুভিত্তিক স্বাস্থ্য সমস্যার প্রবণতা নির্ধারণ।

৫. শিক্ষা:
শিক্ষার্থীদের ফলাফলের প্রবণতা এবং নাম লেখানোর হার বিশ্লেষণে।

তুলনামূলক বৈশিষ্ট্য

কালীন সারি (Queue)

কালীন সারি হলো একটি ডাটা স্ট্রাকচার যা "প্রথমে আসলে প্রথমে যাবে" (FIFO: First In, First Out) নীতিতে কাজ করে। এটি এমন একটি ডাটা সংগঠন যেখানে উপাদানগুলো একটি প্রান্তে (পেছন) যোগ করা হয় এবং অন্য প্রান্তে (সামনে) থেকে সরানো হয়।

কালীন সারির উপাদানসমূহ

কালীন সারির কার্যপ্রণালী বুঝতে এর উপাদান বা উপাংশগুলো জানা গুরুত্বপূর্ণ। কালীন সারির প্রধান উপাদানগুলো হলো:

১. ফ্রন্ট (Front):

• ফ্রন্ট হলো কালীন সারির প্রথম উপাদান।
• এখান থেকে উপাদান সরানো (Dequeue) হয়।

২. রিয়ার বা পেছন (Rear/Back):

• রিয়ার হলো কালীন সারির শেষ প্রান্ত।
• এখানে নতুন উপাদান যোগ করা (Enqueue) হয়।

৩. কালীন সারির দৈর্ঘ্য (Length):

• সারিতে কতগুলো উপাদান রয়েছে তা বোঝানোর জন্য এটি ব্যবহৃত হয়।

৪. সারির সর্বোচ্চ আকার (Capacity):

• নির্ধারণ করে যে একটি কালীন সারি কতগুলো উপাদান ধারণ করতে পারে।

৫. অপারেশন:

কালীন সারিতে উপাদান সংযোজন এবং অপসারণের জন্য নিম্নলিখিত অপারেশনগুলো থাকে:

• এনকিউ (Enqueue):
  নতুন উপাদান যোগ করা হয়।
  উদাহরণ: পেছন থেকে নতুন ডাটা যোগ করা।
• ডিকিউ (Dequeue):
  প্রথম উপাদানটি সরিয়ে ফেলা হয়।
  উদাহরণ: সামনের দিকের ডাটা সরিয়ে ফেলা।
• ফ্রন্ট():
  ফ্রন্টে থাকা উপাদানটি দেখা বা রিটার্ন করার জন্য ব্যবহৃত হয়।
• ইম্পটি চেক (IsEmpty):
  চেক করে যে সারিটি ফাঁকা কিনা।
• পূর্ণতা চেক (IsFull):
  চেক করে যে সারিটি পূর্ণ কিনা।

কালীন সারির প্রকারভেদ

কালীন সারির কার্যপ্রণালী এবং প্রয়োগ অনুসারে এটি বিভিন্ন প্রকারে বিভক্ত:

১. সাধারণ কালীন সারি (Simple Queue):

• FIFO নীতিতে কাজ করে।

২. বৃত্তাকার কালীন সারি (Circular Queue):

• রিয়ার যখন সর্বোচ্চ আকারে পৌঁছে যায়, তখন এটি প্রথমে ফিরে যায় (circular) এবং নতুন উপাদান যোগ হয়।

৩. অগ্রাধিকার কালীন সারি (Priority Queue):

• প্রতিটি উপাদানের একটি অগ্রাধিকার মান থাকে এবং অগ্রাধিকার অনুযায়ী উপাদানগুলো প্রক্রিয়াকরণ হয়।

৪. দ্বি-প্রান্ত কালীন সারি (Deque):

• এখানে উপাদান যোগ ও সরানো উভয়ই ফ্রন্ট এবং রিয়ার থেকে করা যায়।

সারসংক্ষেপ

কালীন সারি একটি গুরুত্বপূর্ণ ডাটা স্ট্রাকচার যা FIFO নীতিতে কাজ করে। এর প্রধান উপাদান হলো ফ্রন্ট, রিয়ার, দৈর্ঘ্য, এবং ক্ষমতা। কালীন সারির কার্যপ্রণালী বিভিন্ন অপারেশন এবং এর প্রকারভেদ, যেমন সাধারণ, বৃত্তাকার, অগ্রাধিকার, এবং দ্বি-প্রান্ত সারির মাধ্যমে আরও কার্যকরভাবে ব্যবহৃত হয়।

নির্ভরণের ব্যবহার (Uses of Correlation)

নির্ভরণ বা সংশ্লেষ (Correlation) পরিসংখ্যান এবং ডেটা বিশ্লেষণের একটি গুরুত্বপূর্ণ পদ্ধতি, যা ভেরিয়েবলগুলোর মধ্যে সম্পর্ক নির্ধারণে ব্যবহৃত হয়। এটি বিভিন্ন ক্ষেত্রে সিদ্ধান্ত গ্রহণ, গবেষণা এবং পূর্বাভাসে গুরুত্বপূর্ণ ভূমিকা পালন করে।

নির্ভরণের প্রধান ব্যবহারসমূহ

১. ভেরিয়েবলের সম্পর্ক নির্ধারণ

• নির্ভরণ ব্যবহার করে দুটি ভেরিয়েবলের মধ্যে সম্পর্কের প্রকৃতি (ধনাত্মক, ঋণাত্মক বা শূন্য) এবং তীব্রতা নির্ধারণ করা যায়।
• উদাহরণ:
  • উচ্চতা ও ওজনের মধ্যে সম্পর্ক।
  • আয়ের পরিমাণ ও ব্যয়ের মধ্যে সম্পর্ক।

২. ভবিষ্যদ্বাণী বা পূর্বাভাস

• নির্ভরণ সাহায্য করে এক ভেরিয়েবল থেকে অন্য ভেরিয়েবলের মান পূর্বাভাস করতে।
• উদাহরণ:
  • আবহাওয়ার পরিবর্তনের সাথে কৃষিজ উৎপাদনের ভবিষ্যদ্বাণী।
  • বিজ্ঞাপন ব্যয়ের ভিত্তিতে বিক্রির পরিমাণ অনুমান।

৩. গবেষণার সহায়ক

• গবেষণায় বিভিন্ন ভেরিয়েবলের সম্পর্ক খুঁজে বের করতে নির্ভরণ একটি গুরুত্বপূর্ণ ভূমিকা পালন করে।
• উদাহরণ:
  • শিক্ষাগত অর্জন এবং ব্যক্তিগত দক্ষতার মধ্যে সম্পর্ক নির্ধারণ।
  • রোগ ও জীবনযাপনের অভ্যাসের সম্পর্ক নিয়ে গবেষণা।

৪. ডেটা বিশ্লেষণে ব্যবহার

• বিভিন্ন ক্ষেত্রের ডেটা বিশ্লেষণে নির্ভরণ ব্যবহৃত হয়:
  • অর্থনীতি: মুদ্রাস্ফীতি এবং বেকারত্বের মধ্যে সম্পর্ক।
  • সমাজবিজ্ঞান: সামাজিক অবস্থা এবং জীবনযাত্রার মানের মধ্যে সম্পর্ক।

৫. ব্যবসায়িক সিদ্ধান্ত গ্রহণ

• ব্যবসায় নির্ভরণ ব্যবহার করে বিভিন্ন কার্যক্রমের মধ্যে সম্পর্ক নির্ধারণ করা হয়, যা কৌশলগত সিদ্ধান্ত গ্রহণে সহায়তা করে।
• উদাহরণ:
  • পণ্যের দাম এবং বিক্রির পরিমাণের সম্পর্ক বিশ্লেষণ।
  • গ্রাহকদের সন্তুষ্টি এবং গ্রাহক ধরে রাখার মধ্যে সম্পর্ক।

৬. পাঠ্যক্রম উন্নয়ন

• শিক্ষাক্ষেত্রে নির্ভরণ ব্যবহার করে শিক্ষার্থীদের ফলাফল এবং তাদের পড়াশোনার পদ্ধতির মধ্যে সম্পর্ক বিশ্লেষণ করা যায়।
• উদাহরণ:
  • অধ্যয়ন সময় এবং পরীক্ষার ফলাফলের সম্পর্ক।

৭. মেডিকেল গবেষণা

• রোগ ও কারণের সম্পর্ক নির্ধারণে নির্ভরণ গুরুত্বপূর্ণ।
• উদাহরণ:
  • ধূমপান ও ফুসফুস ক্যানসারের মধ্যে সম্পর্ক।
  • খাদ্যাভ্যাস ও হৃদরোগের মধ্যে সম্পর্ক।

সারসংক্ষেপ

নির্ভরণ ভেরিয়েবলের সম্পর্ক বিশ্লেষণ ও সিদ্ধান্ত গ্রহণের একটি শক্তিশালী পদ্ধতি। এটি গবেষণা, ডেটা বিশ্লেষণ, পূর্বাভাস এবং ব্যবসায়িক সিদ্ধান্ত গ্রহণে বহুল ব্যবহৃত হয়। নির্ভরণ সঠিক সম্পর্ক নির্ধারণের মাধ্যমে জটিল সমস্যার সমাধান সহজ করে তোলে।

সাধারণ ধারা (Arithmetic Sequence)

সাধারণ ধারা হলো এমন একটি ধারা যেখানে প্রতিটি পদ (Term) তার পূর্ববর্তী পদের সাথে একটি নির্দিষ্ট স্থির পার্থক্য যোগ করে পাওয়া যায়। এই স্থির পার্থক্যকে ধারা পরিবর্তক বা সাধারণ পার্থক্য (Common Difference) বলে। সাধারণ ধারার প্রতিটি পদ নির্ণয়ের জন্য নির্দিষ্ট সূত্র এবং পদ্ধতি রয়েছে।

সাধারণ ধারা নির্ণয়ের মূল বৈশিষ্ট্য

1. সাধারণ পার্থক্য (d):

   • ধারার দুটি ক্রমিক পদের পার্থক্য স্থির থাকে।

     

2. প্রথম পদ (a):
   • ধারার প্রথম পদকে (a) দ্বারা প্রকাশ করা হয়।

3. সাধারণ ধারা নির্ণয়ের সাধারণ রূপ:

   

সাধারণ ধারা নির্ণয়ের বিভিন্ন পদ্ধতি

১. সূত্র ব্যবহার করে নির্ণয়

• উদাহরণ:
  একটি সাধারণ ধারার প্রথম পদ a = 5, সাধারণ পার্থক্য d = 3। এর n-তম পদ নির্ণয় করুন।

  

২. ক্রমিক পদের ব্যবধান নির্ণয় করে

• যদি ধারার কয়েকটি পদ দেওয়া থাকে, তবে ক্রমিক পদের ব্যবধান বের করে ধারা নির্ণয় করা যায়।

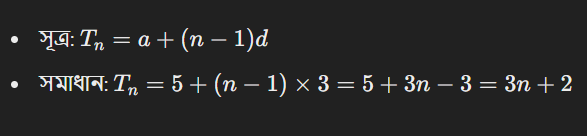
• উদাহরণ:
  

  

৩. ধারা যোগফল ব্যবহার করে

৪. দুই পদ থেকে ধারা নির্ণয়

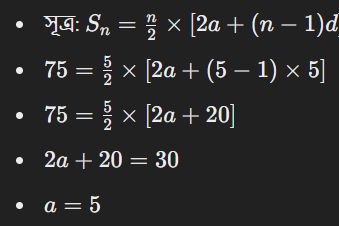
• উদাহরণ:

  

৫. যোগফল ব্যবহার করে শেষ পদ নির্ণয়

• মোট n-টি পদ এবং যোগফল দেওয়া থাকলে শেষ পদ নির্ণয় করা যায়।
• উদাহরণ:
  • 

সারসংক্ষেপ

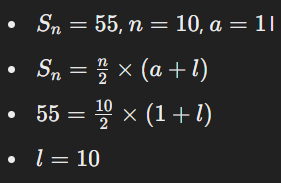
সাধারণ ধারা হলো গাণিতিক পরিসংখ্যানের একটি গুরুত্বপূর্ণ বিষয়, যা পরবর্তী পদ নির্ণয় এবং সমস্যার সমাধানে সহায়ক। বিভিন্ন সূত্র এবং পদ্ধতির সাহায্যে ধারা এবং এর বৈশিষ্ট্য সহজে নির্ণয় করা যায়।

কালীন সারি (Queue) কম্পিউটার বিজ্ঞানের একটি গুরুত্বপূর্ণ ডাটা স্ট্রাকচার, যা প্রথমে আসলে প্রথমে যাবে (First In, First Out - FIFO) নীতির উপর ভিত্তি করে কাজ করে। এটি এমন একটি ক্রম যেখানে উপাদানগুলো একটি প্রান্ত থেকে যুক্ত হয় এবং অন্য প্রান্ত থেকে সরানো হয়। এটি বিভিন্ন প্রোগ্রামিং সমস্যায় কার্যকর সমাধান প্রদান করে।

কালীন সারির ব্যবহার

কালীন সারি বাস্তব জীবনের বিভিন্ন ক্ষেত্রে এবং প্রোগ্রামিংয়ের নানা সমস্যার সমাধানে ব্যবহার করা হয়। এর কয়েকটি গুরুত্বপূর্ণ ব্যবহার নিচে আলোচনা করা হলো:

১. প্রক্রিয়াকরণ ব্যবস্থাপনা (Process Management)

কম্পিউটার সিস্টেমে প্রসেস স্কেডিউলিং-এ কালীন সারি ব্যবহৃত হয়। উদাহরণ:

• প্রিন্টার কিউ: একাধিক ডকুমেন্ট প্রিন্ট করার জন্য প্রিন্টার তাদের কালীন সারিতে সাজায় এবং FIFO ভিত্তিতে প্রিন্ট করে।
• CPU প্রসেস স্কেডিউলিং: বিভিন্ন প্রক্রিয়া কালীন সারিতে রাখা হয় এবং প্রসেসর FIFO নীতিতে এগুলো কার্যকর করে।

২. ডেটা স্ট্রিম হ্যান্ডলিং

কালীন সারি ডেটা স্ট্রিম বা প্রবাহের ক্ষেত্রে ব্যবহৃত হয়:

• ইনপুট/আউটপুট (I/O) ডিভাইস: কী-বোর্ড বা মাউসের ইনপুট একটি কালীন সারিতে সংরক্ষিত হয় এবং পরে প্রসেস করা হয়।
• মেসেজ কিউ: বিভিন্ন মেসেজ বা ডেটা প্যাকেট FIFO নীতিতে সাজানো হয় এবং নেটওয়ার্ক সিস্টেমে পাঠানো হয়।

৩. ব্রাউজার বা সফটওয়্যার ফিচার

• ব্রাউজার হিস্টোরি ম্যানেজমেন্ট: ব্যাক বা ফরওয়ার্ড বাটনের মাধ্যমে ওয়েবপেজ ভিজিটের ক্রম সংরক্ষণের জন্য কালীন সারি ব্যবহৃত হয়।
• অ্যান্ডো/রিডো অপারেশন: FIFO পদ্ধতিতে ক্রিয়াগুলোর তালিকা বজায় রাখা হয়।

৪. অপেক্ষমান সারি মডেলিং (Waiting Line Modeling)

কালীন সারি বিভিন্ন সার্ভিস মডেলিংয়ে ব্যবহার করা হয়:

• এয়ারপোর্ট চেক-ইন: যাত্রীদের FIFO নীতিতে চেক-ইন করা হয়।
• ব্যাংকের সার্ভিস কাউন্টার: গ্রাহকদের কালীন সারি ভিত্তিতে সেবা প্রদান করা হয়।

৫. গ্রাফ ও ট্রি অ্যালগরিদম

কালীন সারি গ্রাফ এবং ট্রি ভিত্তিক অ্যালগরিদমে গুরুত্বপূর্ণ ভূমিকা পালন করে:

• ব্রেডথ-ফার্স্ট সার্চ (BFS): গ্রাফের স্তর অনুসন্ধানের জন্য কালীন সারি ব্যবহৃত হয়।
• লেভেল অর্ডার ট্রাভার্সাল: ট্রি ডেটা স্ট্রাকচারে প্রতিটি লেভেলের উপাদান যাচাই করার জন্য কালীন সারি ব্যবহৃত হয়।

৬. নেটওয়ার্কিং ও মাল্টি-থ্রেডিং

• প্যাকেট সুইচিং: নেটওয়ার্কে ডেটা প্যাকেট FIFO নীতিতে পাঠানো হয়।
• মাল্টি-থ্রেড ম্যানেজমেন্ট: থ্রেডগুলো কালীন সারিতে সাজানো হয় এবং প্রয়োজন অনুযায়ী এক্সিকিউট করা হয়।

৭. রিয়েল-টাইম সিস্টেম

রিয়েল-টাইম অ্যাপ্লিকেশন যেমন:

• টিকিট বুকিং সিস্টেম: বুকিং অনুরোধগুলো কালীন সারিতে জমা হয় এবং FIFO ভিত্তিতে প্রসেস করা হয়।
• ফাস্ট ফুড রেস্টুরেন্ট: অর্ডারগুলো FIFO নীতিতে প্রক্রিয়া করা হয়।

৮. সিমুলেশন

কালীন সারি বিভিন্ন সিমুলেশনে ব্যবহৃত হয়, যেখানে একাধিক ইভেন্ট বা প্রসেস সিরিয়ালভাবে সম্পাদিত হয়:

• ট্রাফিক লাইট সিস্টেমে গাড়ির ক্রম পরিচালনা।

সারসংক্ষেপ

কালীন সারি একটি মৌলিক ডাটা স্ট্রাকচার, যা বাস্তব জীবনের এবং প্রোগ্রামিংয়ের বিভিন্ন ক্ষেত্রে ব্যবহৃত হয়। এটি বিশেষ করে প্রসেস স্কেডিউলিং, ডেটা স্ট্রিম হ্যান্ডলিং, নেটওয়ার্কিং, গ্রাফ অ্যালগরিদম এবং সিমুলেশনে কার্যকর। এর সহজ কিন্তু শক্তিশালী কাঠামো প্রোগ্রামিং সমস্যার সমাধান সহজতর করে।